1.- ¿A que es igual el producto escalar de dos vectores en plano cartesiano?
A = Axi + Ayj + Azk
B = Bxi + Byj + Bzk
teniendo en cuenta que el producto escalar de los vectores :
i · i = j · j = k · k = 1
i · j = i · k = j · k = 0
el resultado de multiplicar escalarmente A por B es:
A · B = Ax· Bx +Ay · By+ Az · Bz
Esta operación no solo nos permite el cálculo de la longitud de los segmentos orientados que representan ( sus módulos ), sino también calcular el ángulo que hay entre ellos. Esto es posible, ya que el producto escalar también se puede hallar en función de sus módulos y del coseno del ángulo que forman mediante la fórmula :
A · B = |A| · |B| · cos (A, B)
2.- Dado una carga eléctrica definida por el vector A y
A = -Ax + 2Ay - 2Az
Hallar:
a) ¿Cual es la magnitud del vector?
b) ¿Calcular la expresión del vector unitario de Ax En dirección de A.?
c) ¿Qué angulo forma A con el eje Z?
a)¿Cual es la magnitud del vector?
A = Ö 9A ²
A = 3A
b)¿Calcular la expresión del vector unitario de Ax En dirección de A.?
U = A / ΙAΙ
ΙAΙ = Ö A² + 4A² + 4A ²
ΙAΙ = Ö 9A ²
ΙAΙ = 3A
U = A / ΙAΙ
U = -Ax / 3Ax + 2Ay / 3A - 2Az / 3A =
U = - 1/3 Ax + 2/3 Ay + 2/3 Az
c)¿Qué angulo forma A con el eje Z?
θ = Tg-¹ Ö 5A ² / -2 A
3.- ¿dado el campo eléctrico cuya expresión viene dada por la expresión
E = 5Ax – 2Ay + Az y el campo magnético H = -3Ax + 4Az
Hallar:
a) Calcular el producto escalar de los dos campos E.H
b) ExH
c) El angulo que hay θEH
a)Calcular el producto escalar de los dos campos E.H
(E · H) = Ex· Hx +Ey · Hy+ Ez · Hz
(E · H) = ( 5Ax – 2Ay + Az ) (-3Ax + 4Az)
(E · H) = ( -15 – 0 + 4 )
(E · H) = ( -11)
b) ExH

Ax Ay Az
ExH = ( 5Ax – 2Ay + Az ) x (-3Ax + 4Az) = 5 -2 1 =
-3 0 4
ExH = -8 Ax – 23Ay - 6Az
c)El ángulo que hay θEH
E = Ö E E =Ö 30
H = Ö H H = Ö (9 + 16)
H = Ö H H = 5
Cosθ = Ax· Bx +Ay · By + Az · Bz
Ö Ax²+ Ay² + Az² Ö Bx²+ By² + Bz²
θEH = Cos-¹0,4016 = 113,6°
4.- Dados los puntos: P1 (1,3,2) a P2 (3,-2,4):
a) Escriba la expresión del campo E que va desde P1 (1,3,2) a P2 (3,-2,4) en coordenadas cartesianas.
Como los componentes del vector son P1 y P2 la expresión del campo vendrá determinado por las coordenadas del extremo menos las coordenadas del origen:
b) Determinar la longitud de P2 a P1
Para calcular la longitud calculamos el modulo del vector E resultante del ejercicio anterior:
E=(2,-5,2) y su modulo viene determinado por:
|E|= √ ((2)2+(-5)2+(2)2)= √ (4+25+4)= |E|= √33
La distancia mas corta desde el origen al vector E, vendrá dado por un vector perpendicular a él y que parta del origen. Para calcularlo, encontremos el ángulo entre E y P1, aplicando la definición de producto escalar:
P1.E = |E|.| P1|.CosαE P1
|P1| = √ ((1)2+(3)2+(2)2) = √ (1+9+4) = √14
P1.E = ((1+3)+(3+(-5))+(2+2) ) = (4-2+4) = 6
Ahora despejamos y sustituimos los valores hayados:
αE P1 = arccos (P1.E / |E|.| P1|) = arccos (6/(√33. √14) = 73.79º
Ahora aplicando la definición del seno hallaremos la altura del triangulo que forma el vector perpendicular a E:
senαE P1 = altura (distancia mas corta del vector E al origen) / | P1|
altura = senαE P1.| P1| = sen 73.79º . √14 = 3.59La distancia más cerca del origen es 3.59.
![[\mathbf A \mathbf B \mathbf C]= \mathbf A \cdot \left( \mathbf B \times \mathbf C \right ) \,](http://upload.wikimedia.org/math/1/b/d/1bd16e79bb75864878e645b29feeb49b.png)


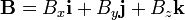

![[ \mathbf A , \mathbf B , \mathbf C ] =
\mathbf A \cdot \left( \mathbf B \times \mathbf C \right ) =
\begin{vmatrix}
A_x & A_y & A_z \\
B_x & B_y & B_z \\
C_x & C_y & C_z \\
\end{vmatrix}](http://upload.wikimedia.org/math/9/9/e/99e1c96e7fbaa2568caa837d7b05c8b8.png)
![[\mathbf A \mathbf B \mathbf C] = [\mathbf B \mathbf C \mathbf A] = [\mathbf C \mathbf A \mathbf B]\,](http://upload.wikimedia.org/math/1/8/0/1802d934def010f631a732b045e0338f.png)
