Electromagnetismo Actividad Nro 2

1.- ¿ A Que es  igual A.( B x C )?

Es llamado producto mixto (también conocido como triple producto escalar) de los vectores A, B y C, en este orden, al escalar que resulta de multiplicar escalarmente por A el producto vectorial de B por C. Esto es

Geométricamente es el área de un paralelepípedo, ejemplo:

El producto mixto de tres vectores dados en función de los vectores cartesianos es:

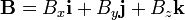
se calcula del siguiente modo:

Es decir que el producto mixto de tres vectores es el determinante de la matriz definida por las componentes cartesianas de los tres vectores.

2.- Demostrar si se cumple: A . (B x C) = B . (C x A) = C . (A x B)

Teniendo en cuenta que el valor de un determinante no varía cuando se realiza un número par de permutaciones entre sus filas (o columnas), se deduce fácilmente que

o sea

de modo que el producto mixto admite la permutación circular entre los vectores que lo integran sin modificar el resultado.

3.- ¿En que condiciones puede ser negativo el producto punto de dos vectores?

      Si el ángulo entre los vectores es mayor que 90º pero menor que 180º el producto es negativo.

4.-Escriba los resultados del producto vectorial y escalar de los vectores A y B, si:

a) A ll B

         

Como los vectores están en paralelo, el ángulo entre ellos es 0º ó 180º, por lo que aplicando la definición nos queda:

A.B = lAl . lBl . cos 0º = lAl . lBl

A.B = lAl . lBl . cos 180º = - lAl . lBl

AxB = lAl . lBl . sen 0º = 0
AxB = lAl . lBl . sen 180º = 0

b) A ┴ B

Como los vectores son perpendiculares, el ángulo entre ellos es 90º ó 270°, por lo que aplicando la definición nos queda:

A.B = lAl . lBl . cos 90º = 0

A.B = lAl . lBl . cos 270º = 0

AxB = lAl . lBl . sen 90º = lAl . lBl

la dirección de Z es saliendo del plano

AxB = lAl . lBl . sen 270º = -lAl . lBl

la dirección de Z es saliendo del plano

c) B ┴ A

Como los vectores son perpendiculares, el ángulo entre ellos es 90º ó 270º, por lo que aplicando la definición nos queda:

A.B = lAl . lBl . cos 90º = 0

A.B = lAl . lBl . cos 270º = 0

AxB = lAl . lBl . sen 90º = lAl . lBl

la dirección de Z es entrando en el plano

AxB = lAl . lBl . sen 270º = -lAl . lBl

la dirección de Z es entrando en el plano

5.- Dado los vectores A y B como se calcula:

a) La componente de A en dirección de B

b) La componente de B en dirección de A

a) La componente de A en la dirección de B es el producto escalar de A por el vector unitario de B:

        AB = A.B 

                   lBl

b) La componente de B en la dirección de B es el producto escalar de A por el vector unitario de A:

        BA = B.A 

                   lAl

6.- Si A.B = A.C; esto implica que B=C

A.B = A.C 

No se puede deducir que B y C sean iguales (aunque pueden serlo) 

Por ejemplo 

A = (1,1,1) 

B = (1,2,3)

 
C = (6,1,-1)

A.B = (1,1,1).(1,2,3) = 1+2+3 = 6 

A.C = (1,1,1).(6,1,-1) = 6+1-1 = 6 

o sea, A.B = A.C, pero B y C son completamente diferentes. 


Si existiera el elemento inverso para el producto escalar sí sería cierto, pero no es así ( en ese caso, multiplicando a ambos lados por el inverso de A, éste término se cancelaría y nos quedaría B = C, pero no es el caso)

7.- Si AxB = AxC; esto implica que B=C.  

De igual manera, “no necesariamente” sí y sólo si y el ángulo entre A y B es igual al ángulo formado por A y C y además el módulo de B y C sean iguales.

Si hacemos la igualdad:

AxB = AxC

lAl . lBl . sen αAB = lAl . lCl . senαAC

lBl . senαAB = lCl . senαAC

Por lo tanto para que se cumpla deben ser idénticos en módulo y ángulo.